A continuación le brindaremos la información pertinente a la lógica.

Concepto de Lógica

La lógica es una ciencia formal que estudia los principios de la demostración e inferencia válida. La palabra deriva del griego antiguo λογική (logike), que significa «dotado de razón, intelectual, dialéctico, argumentativo», que a su vez viene de λόγος (logos), «palabra, pensamiento, idea, argumento, razón o principio».

Así como el objeto de estudio tradicional de la química es la materia, y el de la biología la vida, el de la lógica es la inferencia. La inferencia es el proceso por el cual se derivan conclusiones a partir de premisas. La lógica investiga los principios por los cuales algunas inferencias son aceptables, y otras no. Cuando una inferencia es aceptable, lo es por su estructura lógica, y no por el contenido específico del argumento o el lenguaje utilizado. Por esta razón la lógica se considera una ciencia formal, como la matemática, en vez de una ciencia empírica.

Definición de Preposición.- Es un enunciado al cual se le puede asociar el concepto de verdadero o falso, pero no ambos. La Preposición es el significado de una idea, enunciado, conjunto de palabras o letras a las que se les puede asignar uno y sólo uno de los valores de verdad. En pocas palabras es toda una oración declarativa.

Ejemplos:La luna es cuadrada,7 es un número primo,las arañas son mamíferos.

Las proposiciones pueden ser:

Expresiones Proposicionales.- Son aquellos enunciados a los que no se les puede asignar un valor de verdad. Entre ellos tenemos a los exclamativoss, interrogativos o imperativos.

Ejemplos:¿Cómo te llamas?, Prohibido pasar y Borra el pizarrón.

Enunciados abiertos.- Si en la proposición:"cinco es mayor que tres"(en simbolos es 5 > 3) reemplazamos al número 5 por la letra x, se obtiene la expresión "x es mayor que tres" (x > 3), y si convenimos que x no representa necesiariamente al número 5, sino a un número cualquiera, entonces al enunciado x > 3 se le denomina enunciado abierto.

Proposiciones compuestas conectivas.- Conocido el valor de verdad de ciertas proposiciones, la lógica establece el valor de verdad de otras relacionadas con estas. A estas últimas se les conoce como proposiciones compuestas.

CLases de las proposiciones:
Proposiciones simples o atómicas.- Son aquellas proposiciones que constan o se les puede representar por una sola variable.
Ejemplo:"p:3+6=9".

Proposición compuesta o molecular.- Cuando una preposición consta de dos o más enunciados simples.
Ejemplo:Pitágoras era griego y geómetra.Encontramos dos enunciados, el primero P nos afirma que Pitágoras era griego y el segundo Q que Pitágoras era geómetra.

Lógica Proporcional

La lógica proposicional o lógica de orden cero trata con sistemas lógicos que carecen de cuentificadores, o variables interpretables como entidades. En lógica proposicional si bien no hay signos para variables de tipo entidad, sí existen signos para variables proposicionales (es decir, que pueden ser interpretadas como proposiciones con un valor de verdad de definido), de ahí el nombre proposicional. La lógica proposicional incluye además de variables interpretables como proposiciones simples signos para conectivas lógicas, por lo que dentro de este tipo de lógica puede analizarse la inferencia lógica de proposiciones a partir de proposiciones, pero sin tener en cuenta la estructura interna de las proposiciones más simples.

Una lógica proposicional es un sistema formal cuyos elementos más simples representan proposiciones, y cuyas constantes lógicas, llamadas conectivas, representan operaciones sobre proposiciones, capaces de formar otras proposiciones de mayor complejidad.

Notación y Conectivos Lógicos:

Negacion.- Si p es una preposición, entonces"no p" es la negación de p y se denota por: p
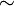Ejemplo:P: hoy es martes y 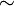p es hoy no es martes.

Como sinónimos de no se utilizan las siguientes expresiones:No es cierto que ...., No es el caso que ...., Es falso que ...., No sucede que ....,etc.

Tabla de certeza o tabla de verdad de la negación.-

 p  p

                              v    f
                                                                            f           v

Conjunción "Y".- La conjunción de dos proposiciones se forma insertando la palabra "Y" entre ellas.

Ejemplo:"Hoy es día de fiesta y ameneció lloviendo", "Me llamo Rosmary y soy Psicopedagoga", "Te llamas Carmen y eres técnico en Artes de Fuego".

Si p y q son proposciones, se llama conjunción de p y q a la proposición"p y q " y se denota por: pq.

Tabla de certeza o tabla de verdad de la conjunción.- 

p  q  pq

                            v  v   v

                            v  f   f

                            f  v   f

                            f  v   f

Se toman como sinónimos de la conjunción:Además, pero , sin embargo, aunque, también, aún, a la vez y no obstante.

Disyunción"O".- La disyunción de dos preposiciones se forma insertando la palabra"o" entre ellas.

Ejemplo:"Hoy es día de fiesta o amaneció lloviendo", "Me llamo Rosmary o soy Psicopedagoga", " Te llamas Carmen o eres técnico en Artes de Fuego".

Si p y q son proposiciones, se llama disyución de p y q a la proposcion compuesta "p o q" y se denota por: p q.

Tabla de certeza o tabla de verdad de la disyunción.-

p  q  pq

                            v  v   v

                            v  f   v

                            f  v   v

                            f  f   f

Condicional.- Si p y q son proposiciones, se llama condicional de p y q a la proposición compuesta"si p entonces q" y se denota por: p q.

Ejemplos:Si no llueve entonces iremos a la playa,Si me gano la lotería entonces me voy de viaje, Si no estudio entonces no aprobaré lógica, etc.

Tabla de certeza o tabla de verdad de la condicional.-

p  q  pq

                            v  v   v

                            v  f   f

                            f  v   v

                            f  f   v

Algunas expresiones son:es condición suficiente para, que supone que, cuando, es condicion necesaria para, sólo si, et .

Doble implicación o bicondicional.- Sólo es verdadera si ambas proposiciones tienen el mismo valor de verdad.

Ejemplo:"Está nublado si y sólo si hay nubes visibles".

Tabla de certeza o tabla de verdad de la bicondicional.-

p  q  pq

                            v  v   v

                            v  f   f

                            f  v   f

                            f  f   v

Leyes del álgebra proposicional

En el cálculo proposicional existen algunas tautologias especilamente útiles cuya demostración se reduce a la confección de su correspondiente tabla de verdad, a saber:

Involución.-  -(-p)q

              se lee "no, no P, equivale a P

Idempotencia.- (p-q) p

                                     (p-q) p

Conmutitividad.- Disyución pvq qvq

                Conjunciónpp qp

Asociatividad.- Disyunción (pvp)vr pv (qvr)

                Conjunción   (pq) r    p   (qr)